Pairwise sequence alignment

Understanding Basics

What is pairwise sequence alignment? It is the comparison of two sequences (could be protein or DNA) to find out the similarity between them.

The global sequence alignment focuses on comparing the entire sequence, filling in gaps so that the length of the sequences are equal. The Needleman Wunsch algorithm (named after Samuel B. Needleman and Christian D. Wunsch)is a popular method to do the same.

A Short Note

Distance in biology has always been defined as ‘how different from same?’. Even in computer science, take the example of hamming distance. Look up Levenshtein distance for further understanding. Similarly in the Needleman Wunsch algorithm, the main attempt is to find the minimum number of alterations that can be made to the primary sequence (by adding gaps), so as to obtain a sequence most similar to the secondary one. In nature, you can think of it as the minimum number of mutations that must’ve occurred to the first sequence in order for the second sequence to be formed.

Understanding The Algorithm

The scoring scheme:

The scoring scheme used is as follows:

1. MATCH - this is the value assigned when two characters that are being compared are similar
2. MISMATCH - when two characters are different
3. GAP PENALTY - value given when there is a gap

Since a penalty is being awarded for every gap (ie. every mutation), our objective is to find the alignment with the maximum score. The score values can be obtained from the EDNAFULL Matrix.

The scoring matrix:

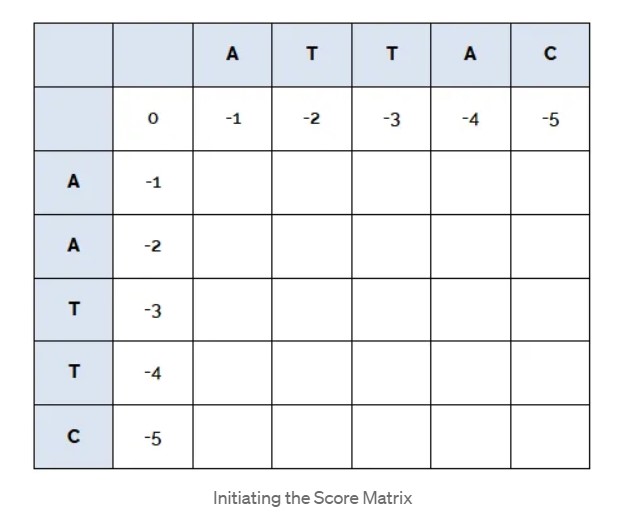
We represent these two sequences in a 2D matrix with the dimensions of the matrix being $(N + 1)(M + 1)$, where $N$ and $M$ are the lengths of the two sequences, and initiate the matrix with the values of the rows as gap penalties times the row number and values of the columns as gap penalty times the column number.

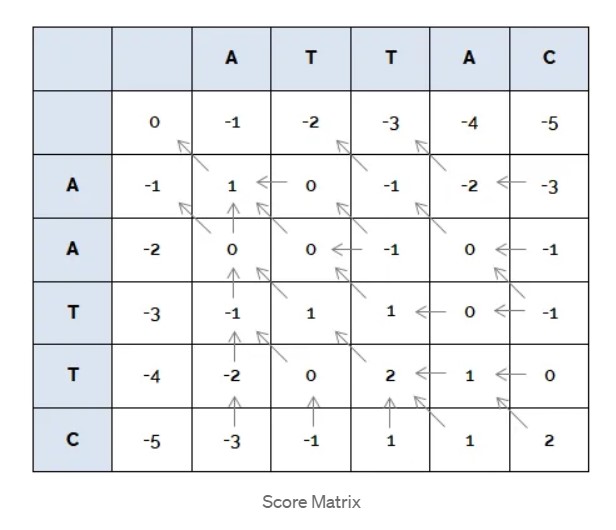
To fill the matrix, start from the top left corner, and keep filling row-wise till you reach the bottom right corner. To find the value for the position (i,j) of the matrix:

\[mat_{i, j} = max \begin{cases} mat_{i-1,j} + gap\_penalty \\ mat_{i,j+1} + gap\_penalty \\ mat_{i-1,j-1} + match\_score & a_i = b_j \\ mat_{i-1,j-1} + mismatch\_score & a_i \ne b_j \end {cases}\]

An implementation of the Needleman Wunsch Algorithm in Python is given below:

def needleman_wunsch(a, b, MATCH_SCORE, INS_DEL_SCORE, SUB_SCORE):
  n = len(a)
  m = len(b)

  # dp[i][j] represents the number of mutations required to change a[:i] to b[:j]
  # By default dp[0][0] = 0 (Converting empty string to an empty string)
  dp = [[-int(1e9)] * (m + 1) for _ in range(n + 1)]
  dp[0][0] = 0

  # par[i][j] points to the cell from in dp from which we came
  # This has no impact on the edit distance, but is useful for further analysis
  par[[(-1, -1) for _ in range(m + 1)] for _ in range(n + 1)]
  
  # Converting a[:i] to an empty string requires deleting every character in the string
  for i in range(n):
    dp[i + 1][0] = dp[i][0] + INS_DEL_SCORE
    par[i + 1][0] = (-1, 0)

  # Converting an empty string into b[:j] requires inserting every character in the string
  for j in range(m):
    dp[0][j + 1] = dp[0][j] + INS_DEL_SCORE
    par[0][j + 1] = (0, -1)

  # For the body of the dp matrix, we have three choices
  # 1. Insert b[j]
  # 2. Delete a[i]
  # 3. Substitute a[i] with b[j] (Note: if a[i] == b[j], we get a match instead of substitution)
  # At any given point, we choose the option which results in the largest value of dp[i + 1][j + 1]
  for i in range(n):
    for j in range(m):
      options = [
        (dp[i][j + 1] + INS_DEL_SCORE, (-1, 0))
        (dp[i + 1][j] + INS_DEL_SCORE, (0, -1))
        (dp[i][j] + (MATCH_SCORE if a[i] == b[j] else SUB_SCORE), (-1, -1))
      ]
      for x, p in options:
        if x > dp[i + 1][j + 1]:
          dp[i + 1][j + 1] = x
          par[i + 1][j + 1] = p

  # dp[n][m] represents the total number of changes/mutations
  return dp, path

Finding the best alignment:

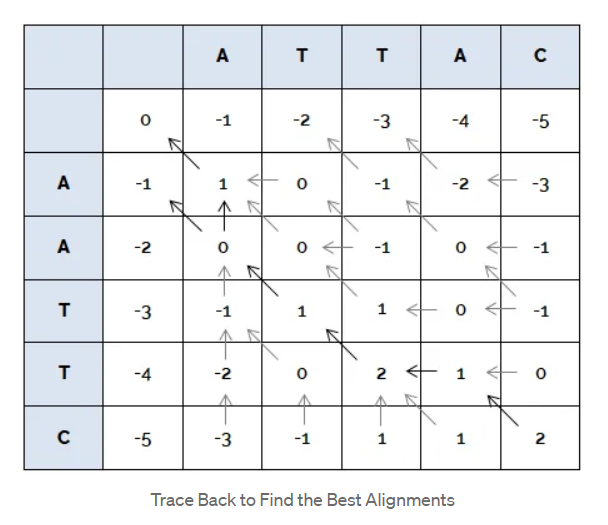
Once the matrix is filled, start from the bottom right corner and work back the arrows till you reach the top left corner. At each place, you can move either top, left or diagonally top-left. Choose the maximum value available of the three.

NOTE: There might be more than one best alignment of the two sequences.

Reconstructing the obtained path:

There is a particular way of writing down these. If we walk back an in the diagonal, then we write down the corresponding characters. If we walk back an arrow to the left, we write the character of the sequence that is written in the horizontal direction, and write a gap ‘-‘ for the sequence written in the vertical direction, and vice versa if we walk back an arrow in the vertical direction.

Here’s what that would look like in Python:

def get_alignment(a, b, par):
  n = len(a)
  m = len(b)
  res = ['', '', '']

  # Start from the bottom right corner of the matrix, (n, m)
  # Move to the top left corner, (0, 0), by following par[i][j] at each step
  # In each step keep adding to the alignment depending on the value of p[i][j]
  # 1. (-1, 0): Insert only a[i] in the alignment and hyphen for b
  # 2. (0, -1): Insert only a[i] in the alignment and hyphen for b
  # 3. (-1, -1): Insert a[i] and b[j] in the alignment
  # Note: In the case of a match, insert a | between the two strings to signify similarity
  x, y = n, m
  while x > 0 and y > 0:
    if par[x][y] == (-1, 0):
      res[0] += a[x - 1]
      res[1] += ' '
      res[2] += '-'
    elif par[x][y] == (-1, 0):
      res[0] += a[x - 1]
      res[1] += ' '
      res[2] += b[y - 1]
    else:
      res[0] += a[x - 1]
      res[1] += '|' if a[x - 1] == b[y - 1] else ' '
      res[2] += b[y - 1]

  # Since we started from (n, m) and ended at (0, 0), we need to reverse our alignment string
  return [i[::-1] for i in res]

Here is a faster implementation in C. code